Blog do HULK: outubro 2010

Remote desktop only on local network: "From: http://ubuntuforums.org/showthread.php?t=1143079&page=2

had the same problem with 9.04, no advanced tab, server was not listening to the port (even default one), but I just found out how to set all this.

To use an alternative port:
run gconf-editor from terminal
in the open window go to:
/desktop/gnome/remote_access
Change the alternative_port value (mine was 5900) to the one you want
Select (check) use_alternative_port

And now, run:
/usr/lib/vino/vino-server
(you can make it run at login by addin the previous line in the: System->Preferences->Startup Applications)

Good Luck!
zensys
June 17th, 2009, 03:01 PM
I had the same problem but was able to solve it by unchecking the option 'configure network automatically to accept connections' This option requires the UPnP feature in your router to be enabled.

Surprisingly (I find computers have a strong resemblance to women) now I also have outside connectivity with the automatically accept connections option checked and UPnP disabled.

Hope this helps more than it confuses!"

Método de integração: "

From Wikibooks, the open-content textbooks collection Calculus | Integration techniques

Jump to: navigation,

A Wikibookian suggests that Solving Integrals by Trigonometric substitution be merged into this book or chapter.

Discuss whether or not this merger should happen on the discussion page.

← Integration techniques/Partial Fraction Decomposition	Calculus	Integration techniques/Tangent Half Angle →
	Integration techniques/Trigonometric Substitution

If the integrand contains a single factor of one of the forms $\sqrt{a^2-x^2} \mbox{ or } \sqrt{a^2+x^2} \mbox{ or } \sqrt{x^2-a^2}$ we can try a trigonometric substitution.

If the integrand contains $\sqrt{a^2-x^2}$ let x = asinθ and use the identity 1 − sin²θ = cos²θ.

If the integrand contains $\sqrt{a^2+x^2}$ let x = atanθ and use the identity 1 + tan²θ = sec²θ.

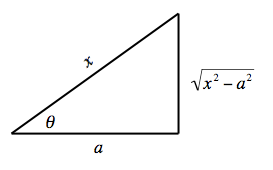
If the integrand contains $\sqrt{x^2-a^2}$ let x = asecθ and use the identity sec²θ − 1 = tan²θ.

[hide]

[edit] Sine substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

If the integrand contains a piece of the form $\sqrt{a^2-x^2}$ we use the substitution

$x=a\sin \theta \quad dx=a \cos \theta d\theta$

This will transform the integrand to a trigonometic function. If the new integrand can't be integrated on sight then the tan-half-angle substitution described below will generally transform it into a more tractable algebraic integrand.

Eg, if the integrand is √(1-x²),

$\begin{matrix} \int_0^1 \sqrt{1-x^2} dx & = & \int_0^{\pi/2} \sqrt{1-\sin^2 \theta} \cos \theta \, d\theta \\ & = & \int_0^{\pi/2} \cos^2 \theta \, d\theta \\ & = & \frac{1}{2} \int_0^{\pi/2} 1+ \cos 2\theta \, d\theta \\ & = & \frac{\pi}{4} \end{matrix}$

If the integrand is √(1+x)/√(1-x), we can rewrite it as

$\sqrt{\frac{1+x}{1-x}} = \sqrt{\frac{1+x}{1+x}\frac{1+x}{1-x}} =\frac{1+x}{\sqrt{1-x^2}}$

Then we can make the substitution

$\begin{matrix} \int_0^a \frac{1+x}{\sqrt{1-x^2}} dx & = & \int_0^\alpha \frac{1+\sin \theta}{\cos \theta} \cos \theta \, d\theta & 0 <a < 1 \\ & = & \int_0^\alpha 1+ \sin \theta \, d\theta & \alpha = \sin^{-1} a \\ & = & \alpha + \left[ - \cos \theta \right]_0^\alpha & \\ & = & \alpha + 1 - \cos \alpha & \\ & = & 1+ \sin^{-1} a - \sqrt{1-a^2} & \\ \end{matrix}$

[edit] Tangent substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

When the integrand contains a piece of the form $\sqrt{a^2+x^2}$ we use the substitution

$x = a \tan \theta \quad \sqrt{x^2+a^2} = a \sec \theta \quad dx = a \sec^2 \theta d\theta$

E.g, if the integrand is (x²+a²)^-3/2 then on making this substitution we find

$\begin{matrix} \int_0^z \left( x^2+a^2 \right)^{-\frac{3}{2}}dx & = & a^{-2} \int_0^\alpha \cos \theta \, d\theta & z>0 \\ & = & a^{-2} \left[ \sin \theta \right]_0^\alpha & \alpha = \tan^{-1} (z/a) \\ & = & a^{-2} \sin \alpha & \\ & = & a^{-2} \frac{z/a}{\sqrt{1+z^2/a^2}} & = \frac{1}{a^2} \frac{z}{\sqrt{a^2+z^2}} \\ \end{matrix}$

If the integral is

$I= \int_0^z \sqrt{x^2+a^2} \quad z>0$

then on making this substitution we find

$\begin{matrix} I & = & a^2 \int_0^\alpha \sec^3 \theta \, d\theta & & & \alpha = \tan^{-1} (z/a) \\ & = & a^2 \int_0^\alpha \sec \theta \, d\tan \theta & & & \\ & = & a^2 [ \sec \theta \tan \theta ]_0^\alpha & - & a^2 \int_0^\alpha \sec \theta \tan^2 \theta \, d\theta & \\ & = & a^2 \sec \alpha \tan \alpha & - & a^2 \int_0^\alpha \sec^3 \theta \, d\theta & + a^2 \int_0^\alpha \sec \theta \, d\theta \\ & = & a^2 \sec \alpha \tan \alpha & - & I & + a^2 \int_0^\alpha \sec \theta \, d\theta \\ \end{matrix}$

After integrating by parts, and using trigonometric identities, we've ended up with an expression involving the original integral. In cases like this we must now rearrange the equation so that the original integral is on one side only

$\begin{matrix} I & = & \frac{1}{2}a^2 \sec \alpha \tan \alpha & + & \frac{1}{2}a^2 \int_0^\alpha \sec \theta \, d\theta \\ & = & \frac{1}{2}a^2 \sec \alpha \tan \alpha & + & \frac{1}{2}a^2 \left[ \ln \left( \sec \theta + \tan \theta \right) \right]_0^\alpha \\ & = & \frac{1}{2}a^2 \sec \alpha \tan \alpha & + & \frac{1}{2}a^2 \ln \left( \sec \alpha + \tan \alpha \right) \\ & = & \frac{1}{2}a^2 \left( \sqrt{1+\frac{z^2}{a^2}} \right) \frac{z}{a} & + & \frac{1}{2}a^2 \ln \left( \sqrt{1+\frac{z^2}{a^2}}+\frac{z}{a} \right) \\ & = & \frac{1}{2}z\sqrt{z^2+a^2} & + & \frac{1}{2}a^2 \ln \left(\frac{z}{a} + \sqrt{1+\frac{z^2}{a^2}} \right) \\ \end{matrix}$

As we would expect from the integrand, this is approximately z²/2 for large z.

[edit] Secant substitution

This substitution is easily derived from a triangle, using the Pythagorean Theorem.

If the integrand contains a factor of the form $\sqrt{x^2-a^2}$ we use the substitution

$x = a \sec \theta \quad dx = a \sec \theta \tan \theta d\theta \quad \sqrt{x^2-a^2} = a \tan \theta.$

[edit] Example 1

Find $\int_1^z \frac{\sqrt{x^2-1}}{x}dx.$

$\begin{matrix} \int_1^z \frac{\sqrt{x^2-1}}{x}dx & = & \int_1^\alpha \frac{\tan \theta }{\sec \theta }\sec \theta \tan \theta \,d\theta & z>1 \\ & = & \int_0^\alpha \tan^2 \theta \, d\theta & \alpha = \sec^{-1} z \\ & = & \left[ \tan \theta -\theta \right]_0^\alpha & \tan \alpha = \sqrt{\sec^2 \alpha -1} \\ & =& \tan \alpha -\alpha & \tan \alpha = \sqrt{z^2-1} \\ & =& \sqrt{z^2-1} - \sec^{-1} z & \\ \end{matrix}$

[edit] Example 2

Find $\int_1^z \frac{\sqrt{x^2-1}}{x^2} dx.$

$\begin{matrix} \int_1^z \frac{\sqrt{x^2-1}}{x^2}dx & = & \int_1^\alpha \frac{\tan \theta}{\sec^2 \theta}\sec \theta \tan \theta \, d\theta & z>1 \\ & = & \int_0^\alpha \frac{\sin^2 \theta}{\cos \theta} d\theta & \alpha = \sec^{-1} z \\ \end{matrix}$

We can now integrate by parts

$\begin{matrix} \int_1^z \frac{\sqrt{x^2-1}}{x^2}dx & = & -\left[ \tan \theta \cos \theta \right]_0^\alpha + \int_0^\alpha \sec \theta \, d\theta \\ & = & -\sin \alpha +\left[ \ln (\sec \theta + \tan \theta ) \right]_0^\alpha \\ & = & \ln (\sec \alpha + \tan \alpha ) - \sin \alpha \\ & = & \ln (z+ \sqrt{z^2-1} ) - \frac{\sqrt{z^2-1}}{z}\\ \end{matrix}$

Navigation: Main Page · Precalculus · Limits · Differentiation · Integration · Parametric and Polar Equations · Sequences and Series · Multivariable Calculus & Differential Equations · Extensions · References

Retrieved from 'http://en.wikibooks.org/wiki/Calculus/Integration_techniques/Trigonometric_Substitution'

Categories: Books to be merged | Calculus (book)

Blog do HULK

sexta-feira, 22 de outubro de 2010

No Retreat, No Surrender !!!

quinta-feira, 21 de outubro de 2010

Remote desktop only on local network

segunda-feira, 4 de outubro de 2010

Método de integração

Contents

[edit] Sine substitution

[edit] Tangent substitution

[edit] Secant substitution

[edit] Example 1

[edit] Example 2

Seguidores

Quem sou eu

Arquivo do blog

jorgehulk's shared items

Onde eu estou?

Google Plus